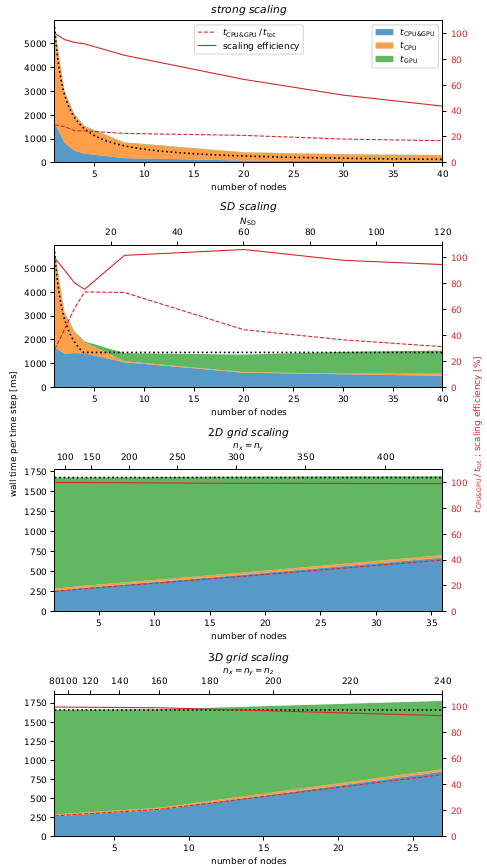
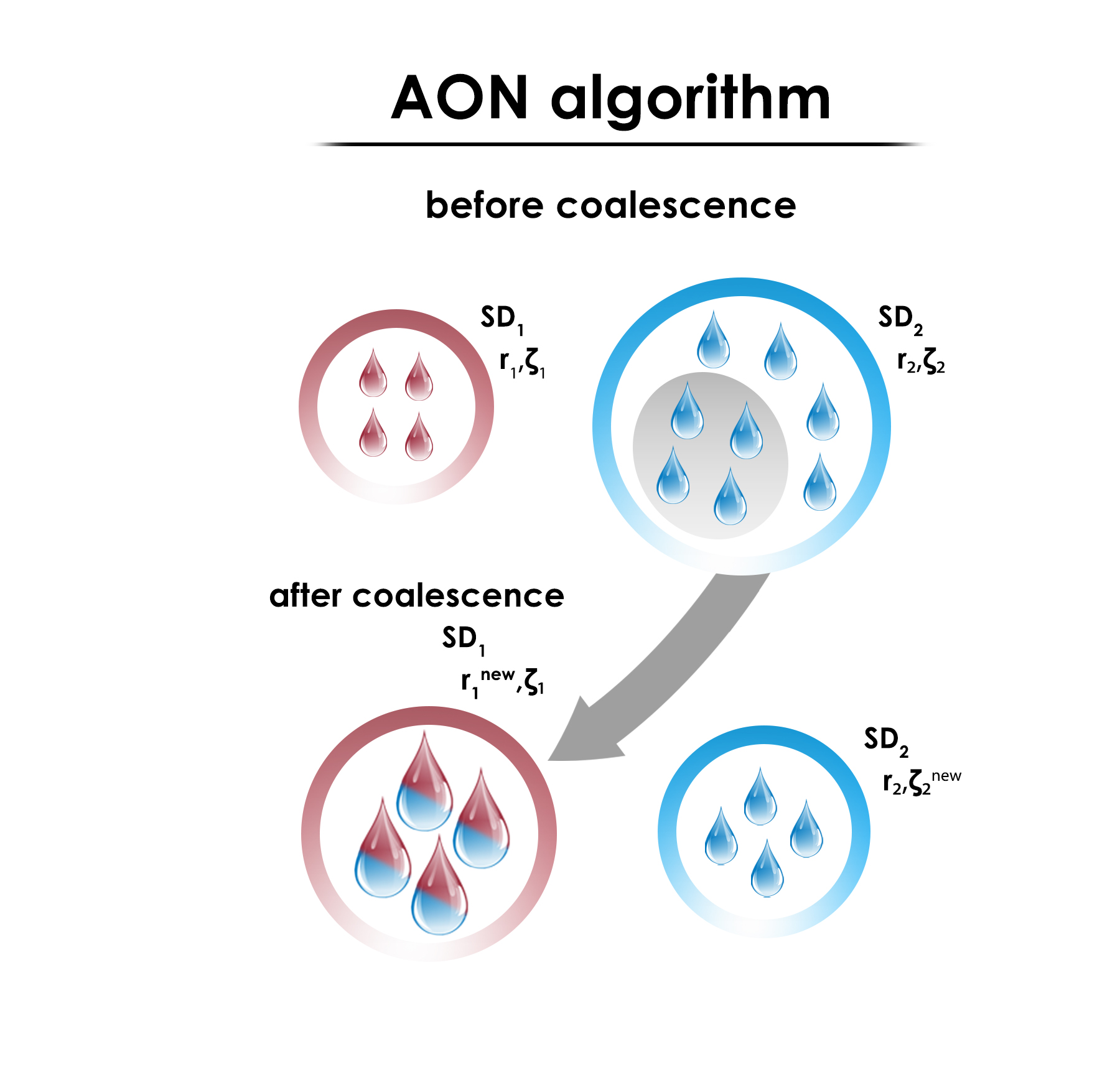
In this description, we assume that the probability of collision between a pair of particles is known, and it is proportional to the coalescence kernel.
The All Or Nothing (AON) algorithm is designed to accurately predict the expected number of collisions while keeping the number of super-droplets (SDs) constant.
However, a drawback of the AON algorithm is that it introduces a larger variance in the number of collisions compared to the real variance.
Initially, AON was developed to mimic the real phenomena of droplet collision-coalescence events, enabling one-to-one simulations where each SD represents a single real droplet.
Unfortunately, the computational requirements for one-to-one simulations exceed the capabilities of currently available HPC.
Therefore, the initialization method for SDs, which represents many real droplets, plays an important role in simulations.
Various initialization algorithms exist, and they can be categorized into two groups.
The first group ensures that all SDs have the same multiplicity, and their radii are randomly chosen based on the cumulative distribution function (CDF).
In the second method, we specify the desired number of SDs within the grid box and randomly assign radii based on any distribution, which determines the multiplicity of each SD.
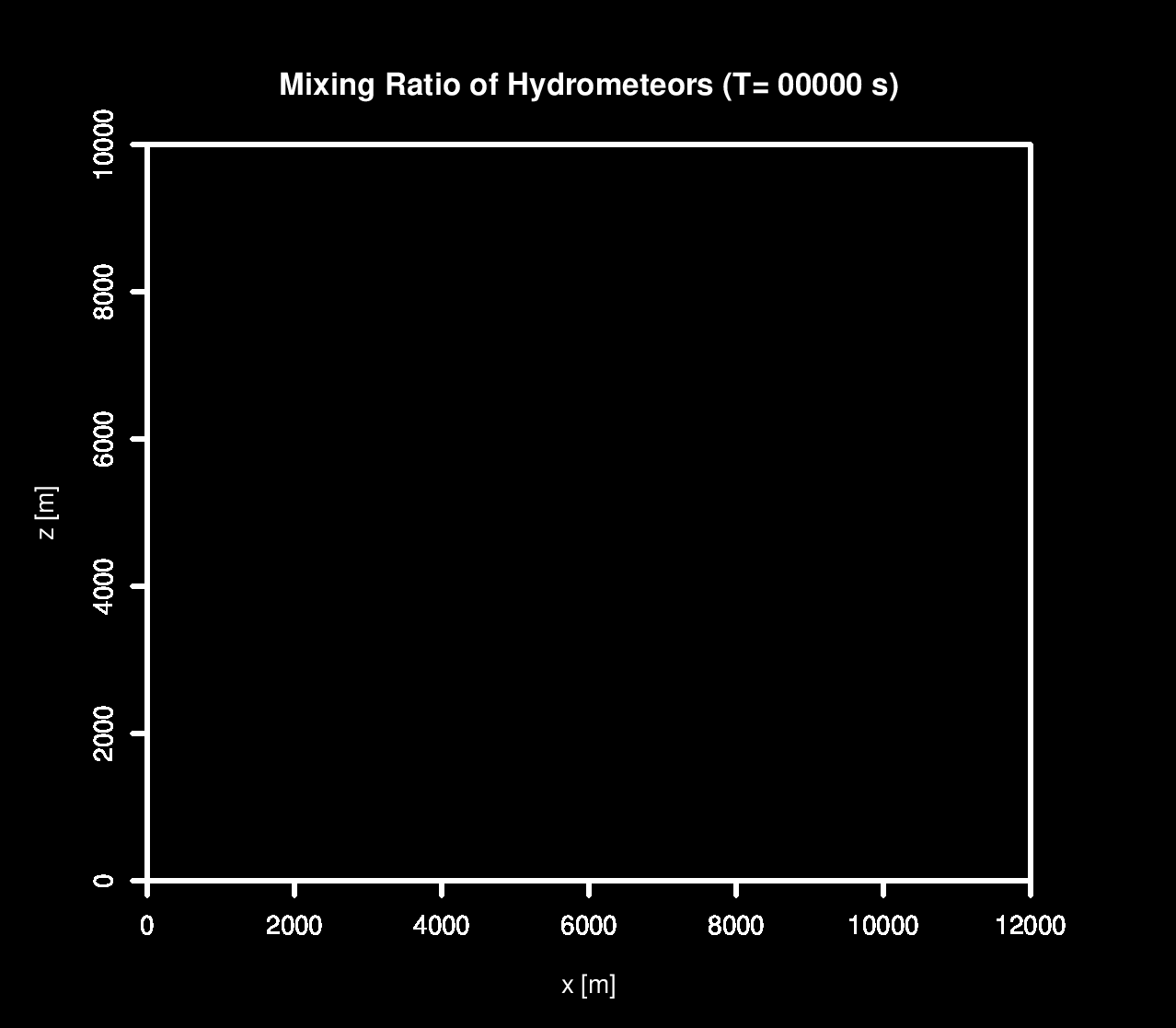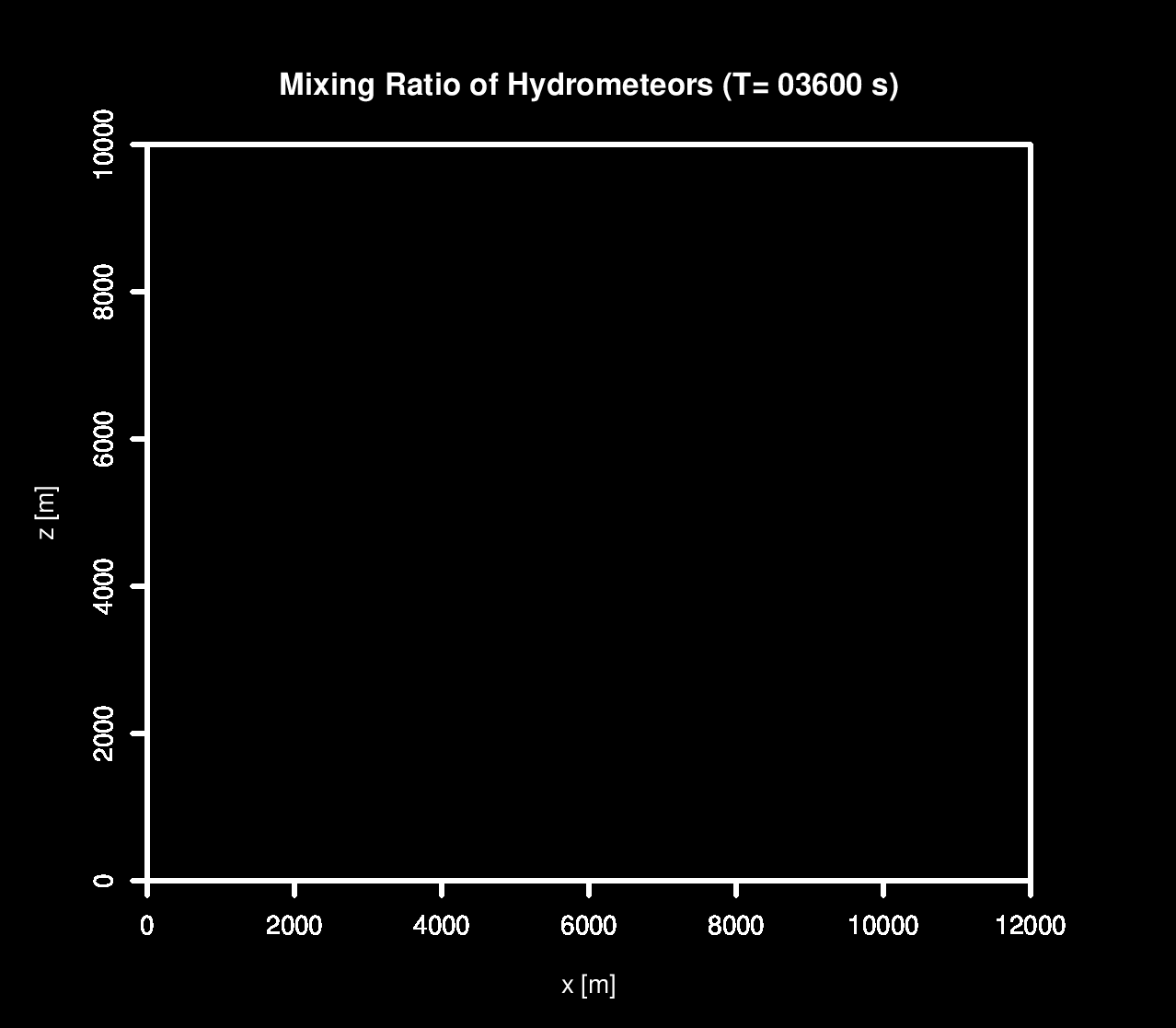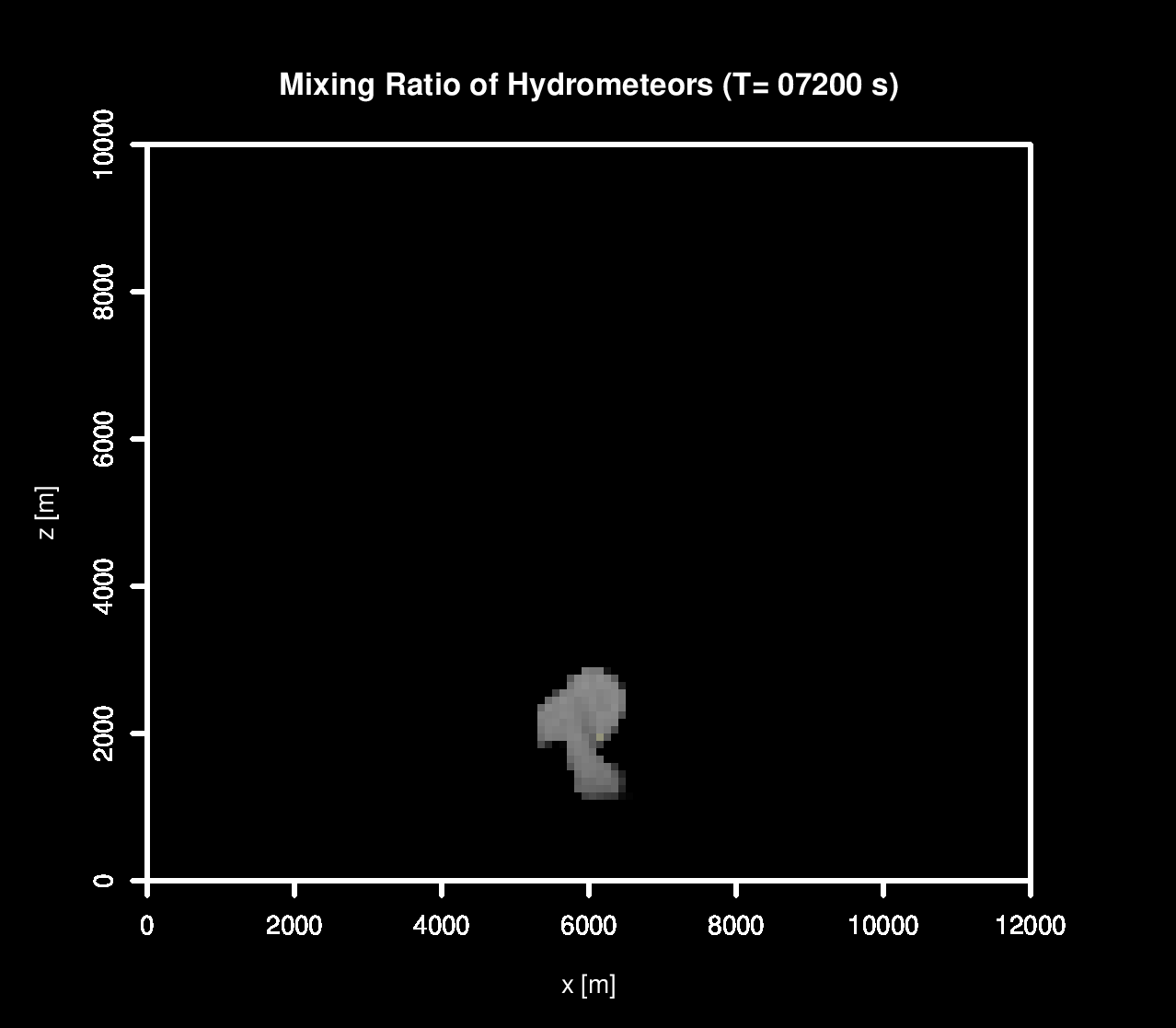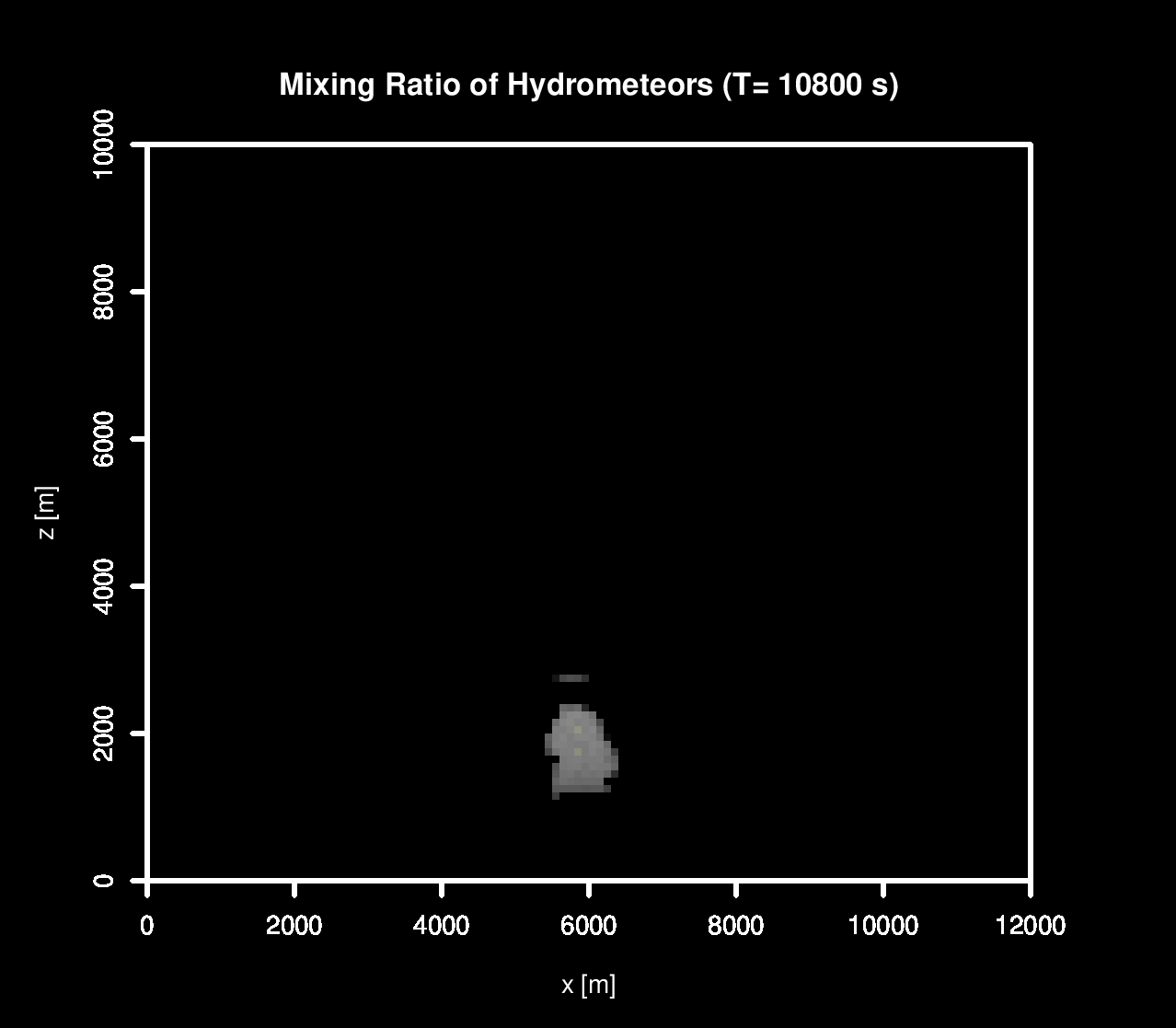
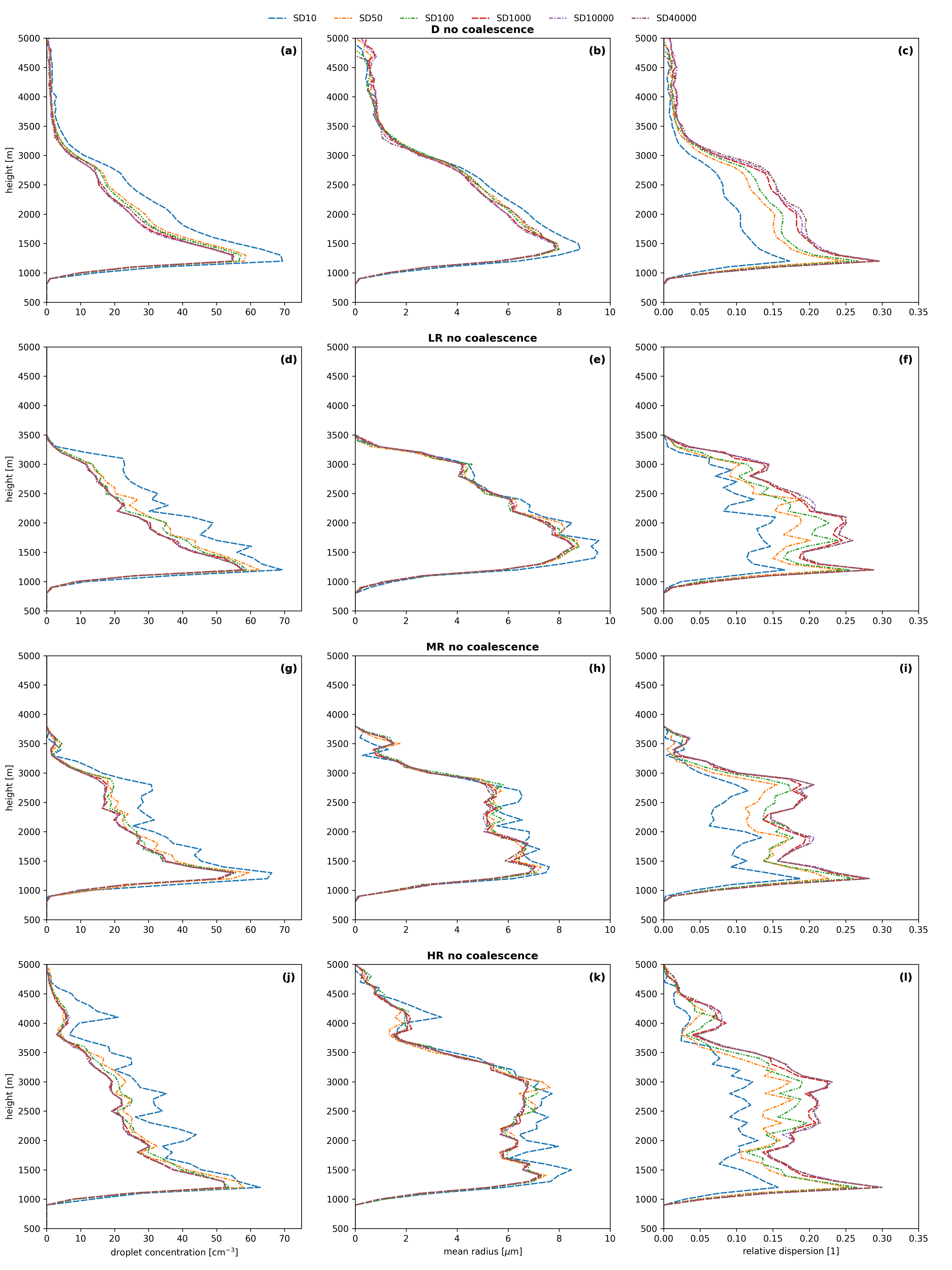
In my research, I performed sensitivity tests on the All Or Nothing (AON) algorithm within the context of an isolated Cumulus Congestus Cloud, following the setup described by Lasher-Trap et al. (2005).
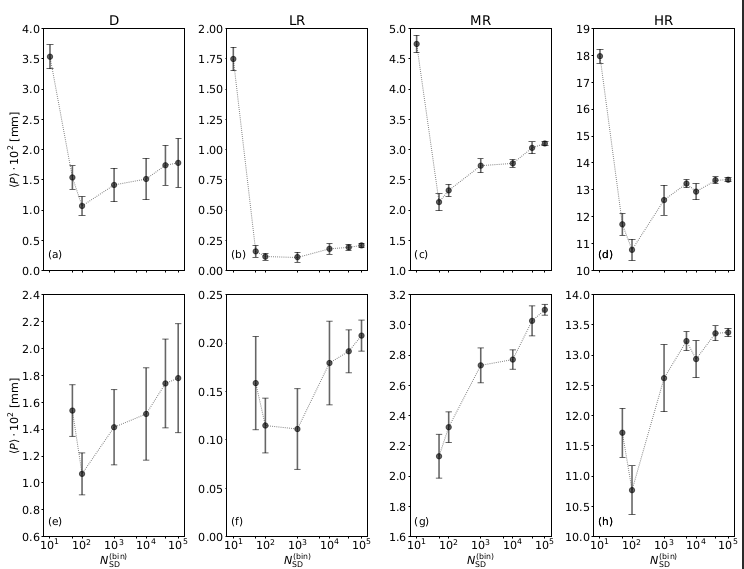
Specifically, I examined the impact of the number of SDs per grid box, SD initialization method, and coalescence substep on the behavior of the AON algorithm.
Additionally, to advance my research further, I examined the behavior of the AON algorithm under varying precipitation conditions, including scenarios with minimal rainfall ('LR'), moderate rainfall ('MR'), and heavy precipitation ('HR').
Throughout these simulations, the velocity field remained consistent across all scenarios, with differences only in the microphysics aspects of the simulations.
As part of the investigation, I also performed fully dynamical simulations.
One of the main objectives of this research was to analyze how the random perturbation in the AON algorithm influences the spread of the obtained results.